Lesson 21: Triad
Inversions
Let's review a little of what we learned about triads
in some previous lessons. In Lesson 15 you learned that
a triad is a three-note chord in which there is a root, a third and
a fifth. In Lesson 17
you learned about four different kinds of triads: major, minor, augmented
and diminished. You should at this point have a clear understanding
of the structure of triads. If you don't, go back and reread those
lessons before continuing with this lesson.
In all of the triads you have seen so far, the root
has been on the bottom, the third in the middle, and the fifth on top,
like this one: 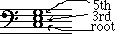 I'. That's because 'C' is the first note in a C-major scale.
Building a triad on the first note of a scale gives us a I-chord. A I-chord in C-major has a 'C',
'E' and 'G.
We can show exactly how the notes are ordered in a
triad by indicating the intervals above the bass (bottom) note. For
example, in the triad above, and indeed with all triads in root
position, there is a note three notes above the bass, and a note five
notes above the bass. Therefore, to be technically precise, we could call
this triad: 
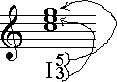
The '5' indicates the 'G' which is the interval of a
5th above the bottom note. The '3' indicates the 'E' which is the interval
of a 3rd above the bottom note. However, for root position chords,the
common practice is to just use the Roman numeral. If you see a chord with
a Roman numeral and no small "Arabic" numbers after it, it is a root
position chord. So the chord above could be represented by just using the
Roman numeral:
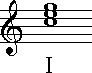
Here are triads built on the notes of a C-major scale,
all in root position. We know they are root position because: 1) there are
no small Arabic numbers after the Roman numeral; and 2) the chord is made
up of a root, 3rd and 5th with the root on the bottom:
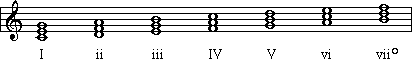
Remember, we use upper-case Roman numerals to indicate
major and augmented triads, and lower-case letters to indicate minor and
diminished.
It is possible to "reposition" the chords above so
that the root is no longer on the bottom. For example, you could write
each one of the chords above in such a way that the 3rd of each
chord is on the bottom:
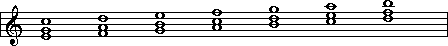
The Roman numeral will stay the same for each chord,
because the components of each chord (1,3,5) are still present. It's just
that now they are in a different order. So how do we indicate this kind of
triad, where the same notes exist as for root position chords (1-3-5), but
that the 3rd is on the bottom? If you count upward from the bottom note,
you will discover that the other notes are a 3rd and a 6th above
it:
Such chords are called 1st inversion chords. It
is traditional with 1st inversion chords to drop the little '3' after the
Roman numeral, and just use the '6'. So the triads shown above would be
labeled like this:
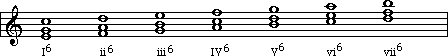
It is also possible to rearrange root position triads
so that the 5th is on the bottom:
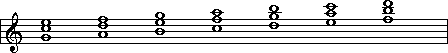
We use the same Roman numerals as before, to label
these triads. The first triad is made up of a C, E and G, and so it gets a
Roman numeral 'I', and so on. If you count upward
from the bottom note, you will find that the other notes are a 4th and a
6th above it:
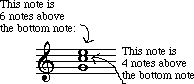
Such chords are called 2nd inversion chords.
All of the triads of a C-major scale would be labeled like
this:
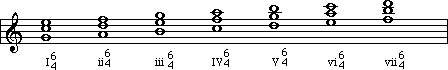
Let's sum up what we've learned in this lesson so far:
Here are some triads properly analyzed. Study each one, and be certain
that you understand how each one has been analyzed before trying the
quiz:
Notice that in the final example the V-chord has been
made major by raising the 3rd. All dominant chords must be major.
Two more points about inversions: All of the examples above have used
close spacing. That means that all of the tones are within an
octave of each other. But it is possible to spread out the notes into
different octaves (open spacing). Also, you will be required to
analyze triads in which some of the tones appear more than once in the
triad.Look at these triads- they are all 2nd inversion triads:
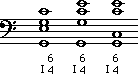
They are all I-chords because they all have a C, E and
G. They are all 6-4 chords (2nd inversion) because they all have the 5th
(g) as their lowest note. Easy! | 
The Music Room